Schnittpunkt zweier linearer Funktionen
Aufgabe Neue Aufgabe
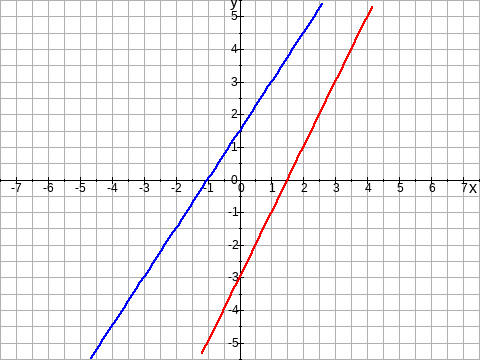
Gegeben seien die linearen Funktionen $f_1(x) = 1{,}5\,x+1{,}5 $ und $f_2(x) = 2\,x-3 $.
Ermittle rechnerisch den Schnittpunkt von $f_1$ und $f_2$. Zeichne die Graphen.
Ablesen der Parameter m und n: Anzeigen
\[ m_1 = 1{,}5 \quad n_1 = 1{,}5 \qquad\qquad m_2 =
2 \quad n_2 = -3 \]
Existenz des Schnittpunktes: Anzeigen
\[ m_1 \neq m_2 \mbox{ und } n_1 \neq n_2 \quad\Longrightarrow\qquad\text{Schnittpunkt muss berechnet werden.} \]
Berechnung durch Gleichsetzen: Anzeigen
\begin{eqnarray*}
f_1(x) & = & f_2(x) \\ 1{,}5\,x+1{,}5 & = & 2\,x-3 \quad \mid \dots\\ & \dots & \\[2mm] x_s & = & \underline{ 9 } \\[1mm] y_s & = & f_1( 9 ) = \underline{ 15
} \\[1mm] S & = & \underline{\underline{ (\, 9 \mid 15 \,) }}
\end{eqnarray*}
Graph: Anzeigen