Integration ganzrationaler Funktionen
Aufgabe Neue Aufgabe
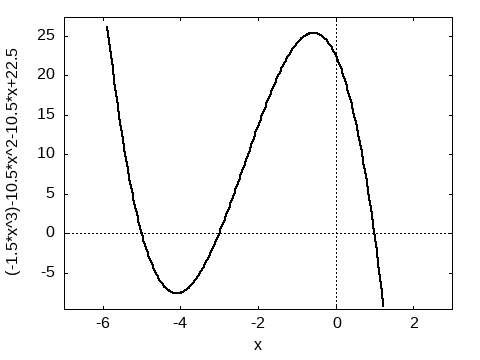
Gegeben sei die Funktion $f(x) = 8\,x-0.5\,x^3 $.
Ermitteln Sie den Inhalt der von $f$ und der $x$-Achse insgesamt eingeschlossenen Fläche.
Nullstellen: Anzeigen
\[ \mathrm{Nullstellen: }
\quad x_1 = -4
\quad x_2 = 0
\quad x_3 = 4
\]
Graph: Anzeigen
Stammfunktion: Anzeigen
\[ F(x) = 4\,x^2-0.125\,x^4 \]
Teilintegrale: Anzeigen
\begin{eqnarray*} \int\limits_{-4}^{0} f(x) \, dx & = & \left[ 4\,x^2-0.125\,x^4
\right]_{-4}^{0} \\ & = & ( 0 ) - ( 32 ) = - 32 \end{eqnarray*}
\begin{eqnarray*} \int\limits_{0}^{4} f(x) \, dx & = & \left[ 4\,x^2-0.125\,x^4
\right]_{0}^{4} \\ & = & ( 32 ) - ( 0 ) = 32 \end{eqnarray*}
Flächenberechnung: Anzeigen
\[ A =
| - 32 | \mathrm{\;FE}
+ | 32 | \mathrm{\;FE}
= 64 \mathrm{\;FE} \]