Fläche zwischen zwei ganzrationalen Funktionen
Aufgabe Neue Aufgabe
Gegeben sind die Funktionen
\begin{eqnarray*} f(x) & = & x^3-4\,x^2-10\,x \\ g(x) & = & -3\,x-10 \end{eqnarray*}Skizzieren Sie die Graphen der beiden Funktionen
und
ermitteln Sie den Inhalt der von $f$ und $g$ insgesamt eingeschlossenen Fläche.
Nullstellen: Anzeigen
\begin{eqnarray*} f(x) : & &
\quad x_1 = 0
\quad x_2 = -1.741
\quad x_3 = 5.741
\\ g(x) : & &
\quad x_1 = -3.333
\end{eqnarray*}
Lokale Extrema/Sattelpunkte: Anzeigen
\begin{eqnarray*}
f(x) : & \quad &
\quad T( 3.594|-41.18)
\quad H( -0.9274|5.036)
\\ g(x) : & \quad &
\end{eqnarray*}
Schnittpunkte: Anzeigen
\[
\quad P_1 = ( -2|-4)
\quad P_2 = ( 1|-13)
\quad P_3 = ( 5|-25)
\]
Graph: Anzeigen
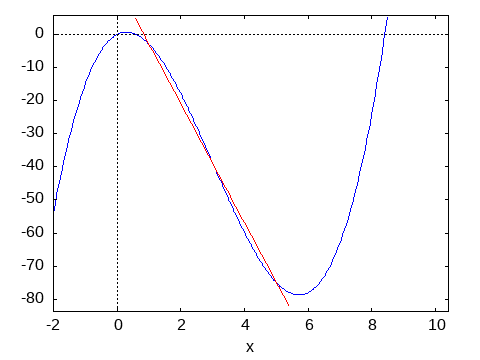
Differenzfunktion: Anzeigen
\[ h(x) = f(x) -g(x) = x^3-4\,x^2-7\,x+10 \]
Stammfunktion: Anzeigen
\[ H(x) = {{x^4}\over{4}}-{{4\,x^3}\over{3}}-{{7\,x^2}\over{2}}+10\,x \]
Teilintegrale: Anzeigen
\begin{eqnarray*} \int\limits_{-2}^{1} h(x) \, dx & = & \left[
{{x^4}\over{4}}-{{4\,x^3}\over{3}}-{{7\,x^2}\over{2}}+10\,x \right]_{-2}^{1} \\ & = & ( 5.416
) - ( - 19.33 ) = 24.75 \end{eqnarray*}
\begin{eqnarray*} \int\limits_{1}^{5} h(x) \, dx & = & \left[
{{x^4}\over{4}}-{{4\,x^3}\over{3}}-{{7\,x^2}\over{2}}+10\,x \right]_{1}^{5} \\ & = & ( - 47.91
) - ( 5.416 ) = - 53.33 \end{eqnarray*}
Flächenberechnung: Anzeigen
\[ A =
| 24.75 | \mathrm{\;FE}
+ | - 53.33 | \mathrm{\;FE}
= 78.08 \mathrm{\;FE} \]