Kurvendiskussion ganzrationaler Funktionen
Aufgabe Neue Aufgabe
Gegeben sei die Funktion $f(x) = x^3-4\,x $
Ermitteln Sie die Eigenschaften der Funktion $f$ und skizzieren Sie den Graphen.
Nullstellen: Anzeigen
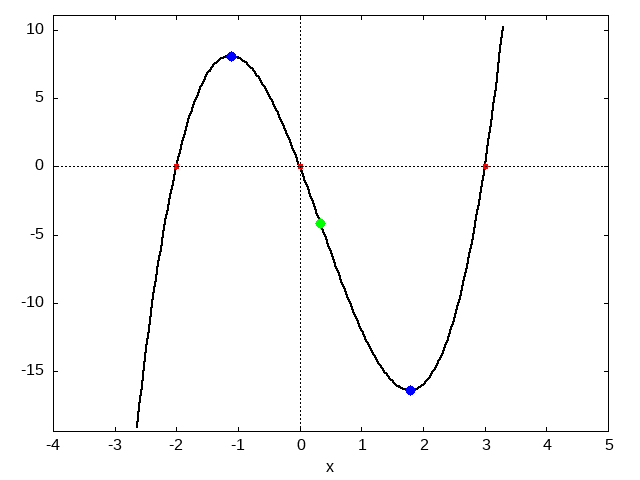
\[ \mathrm{Nullstellen: }
\quad x_1 = -2
\quad x_2 = 0
\quad x_3 = 2
\]
Achsenschnittpunkte: Anzeigen
\[ \mathrm{Achsenschnittpunkte: } \quad
S_1( 0 | 0 )
,\quad S_2( -2 | 0 )
,\quad S_3( 0 | 0 )
,\quad S_4( 2 | 0 )
\]
Symmetrie: Anzeigen
$f$ ist punktsymmetrisch zu $(0|0)$, da gilt: $f(x) = -f(-x)$.
Verhalten im Unendlichen: Anzeigen
\begin{eqnarray*}
\lim\limits_{x \rightarrow +\infty} f(x) & = & \infty \\
\lim\limits_{x \rightarrow -\infty} f(x) & = & -\infty
\end{eqnarray*}
1 und 2. Ableitung: Anzeigen
\begin{eqnarray*}
f'(x) & = & 3\,x^2-4 \\ f''(x) & = & 6\,x
\end{eqnarray*}
Lokale Extrema: Anzeigen
\begin{eqnarray*}
\mathrm{Hochpunkt:} & \quad & H( - 1.15 | 3.07 )\\
\mathrm{Tiefpunkt:} & \quad & T( 1.15 | - 3.07 )\\
\end{eqnarray*}
Wendepunkte: Anzeigen
\[
\mathrm{ Wendepunkt(e):}
\quad W_ 1 ( 0 | 0 )
\]
Graph: Anzeigen
