Tangenten- und Normalengleichung
Aufgabe Neue Aufgabe
Gegeben sei die Funktion $f(x) = 2\,x^3-20\,x^2+58\,x-40 $
Ermitteln Sie die Gleichungen der Tangente und der Normalen bei $x = 4.5 \,$.
Punkt auf Graph bestimmen: Anzeigen
\begin{eqnarray*}
P(\,x\,|\,f(x)\,) & = & P(\, 4.5 \,|\, -1.75 \,)
\end{eqnarray*}
Erste Ableitung und Anstieg der Tangente: Anzeigen
\begin{eqnarray*}
f'(x) & = & 6\,x^2-40\,x+58 \\ m_T = f'(\, 4.5 \,) & = & -0.5
\end{eqnarray*}
Tangentengleichung: Anzeigen
\begin{eqnarray*}
y_T & = & m_T x + n_T \\ -1.75 & = & (-0.5) \cdot 4.5 + n \\ n_T & = & 0.5 \\[2mm] y_T & = &
-0.5 x + 0.5
\end{eqnarray*}
Normalengleichung: Anzeigen
\begin{eqnarray*}
m_N & = & \frac{-1}{m_T} = 2 \\[2mm] y_N & = & m_N x + n_N \\ -1.75 & = & 2 \cdot 4.5
+ n_N \\ n_N & = & -10.75 \\[2mm] y_N & = & 2 x - 10.75
\end{eqnarray*}
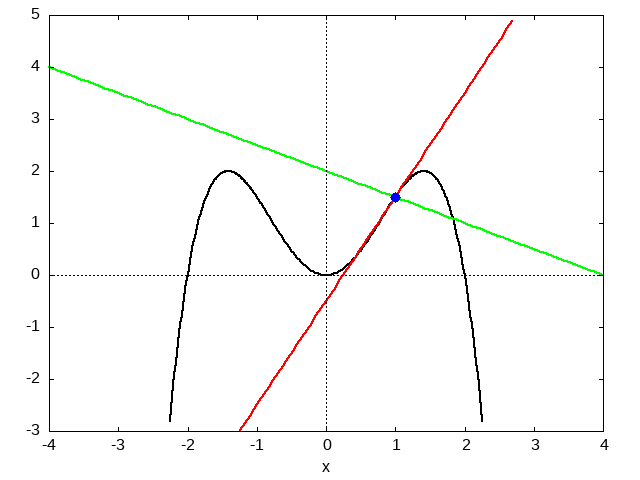
Graph: Anzeigen
