Lineare Funktion durch 2 Punkte (Gleichungssystem)
Aufgabe Neue Aufgabe
Gegeben seien die Punkte $P_1(\, 2{,}5 \mid -1 \,)$ und $P_2(\, -3 \mid 4{,}5 \,)$.
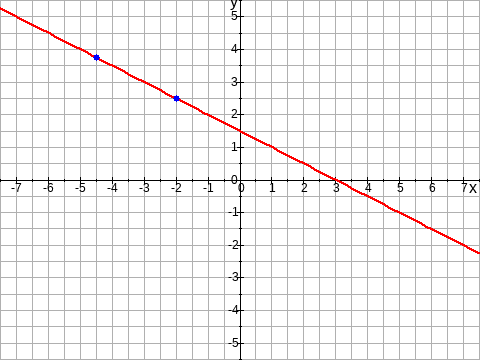
Ermittle rechnerisch die Funktionsgleichung der Geraden durch $P_1$ und $P_2$. Zeichne den Graphen.
Allgemeiner Ansatz, Einsetzen der Punkte: Anzeigen
\[\begin{array}{rrcl}
& y & = & m\cdot x + n \\[2mm] P_1:\; & -1 & = & m\cdot 2{,}5 + n \\[1mm] P_2:\; & 4{,}5 & = & m\cdot (-3) + n \\[1mm]
\end{array}\]
Lösung des Gleichungssystems (Additionsverfahren): Anzeigen
\[\begin{array}{rrcrcl}
I:\; & -1 & = & 2{,}5 m &+& n \\ II:\; & 4{,}5 & = & -3 m &+& n \\ \hline II-I:\; & 5{,}5 & = & -5{,}5 m &+& 0
\end{array}\]
\[\begin{array}{rcll}
-5{,}5 m & = & 5{,}5 & \quad\mid\;\;: (-5{,}5) \\[.5mm] m & = & \underline{ -1 } & \\[.5mm] [\dots]\quad n & = & \underline{ 1{,}5 } & \\[3mm] f(x) & = & 1{,}5-1\,x & \\ \hline
\end{array}\]
Graph: Anzeigen
