Eigenschaften quadratischer Funktionen (Kurvendiskussion)
Aufgabe Neue Aufgabe
Gegeben sei die quadratische Funktion $f(x) = 0{,}25\,x^2-2{,}5\,x+6{,}25 $.
Geben Sie die Eigenschaften von $f$ an und zeichnen Sie den Graphen.
Sie dürfen das Tafelwerk und den Taschenrechner benutzen.
Ablesen der Parameter, Scheitelpunkt: Anzeigen
\[ a = 0{,}25 \qquad b = -2{,}5 \qquad c = 6{,}25 \]
\[ \Longrightarrow\quad S\,(\, -\frac{b}{2a}\mid \frac{4ac-b^2}{4a}\,) \;=\; \underline{S\,(\, 5 \mid 0 \,)} \]
Definitions- und Wertebereich: Anzeigen
\[ D = \mathbf{R} \qquad W = \left\{ y \in \mathbf{R}, y \ge 0 \right\} \]
Monotonie: Anzeigen
Die Funktion ist monoton fallend für $x \le 5 $ und monoton steigend für $x \ge 5 $.
Symmetrie: Anzeigen
Die Funktion ist achsensymmetrisch zur Senkrechten bei $x = 5 $.
Nullstelle(n): Anzeigen
\begin{eqnarray*}
f(x) = 0 & = & 0{,}25\,x^2-2{,}5\,x+6{,}25 \qquad\mid\; : 0{,}25 \\[1mm] 0 & = & x^2-10\,x+25 \\[1mm] x_{1,2} & = & 5 \pm \sqrt{\; 0 \;} \\[2mm] x_0 & = & \underline{5}
\end{eqnarray*}
Achsenschnittpunkte: Anzeigen
\[ S_1(\, 0 \mid 6{,}25 \,)
\qquad S_ 2 (\, 5 \mid 0 \,)
\]
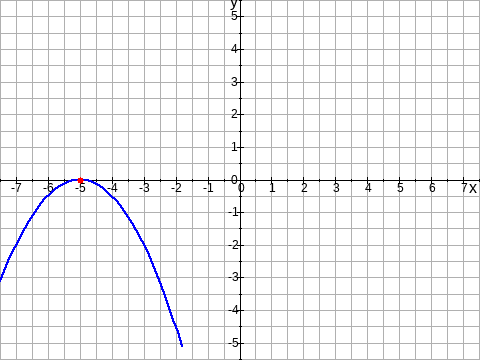
Graph: Anzeigen
